运算放大器稳定性分析——稳定性分析¶
为什么极点/零点处增益变化3dB,相位变为90°?
以简单的低通RC电路为例,增益为A=Zc/(Zc+R),Aol=20lgA。
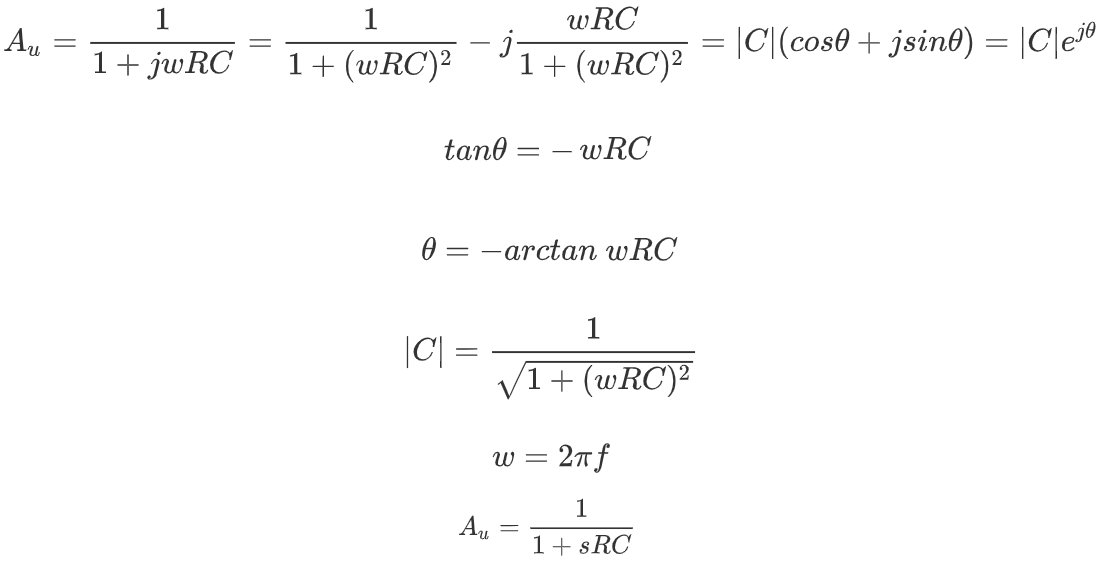
s域中定义了零极点,可见有极点,为-1/RC。
分析幅频特性w:+0->+∞的情况:
w=0时,|C|=1=0dB,Θ=-arctang(0)=0°
w=1/RC时,|C|=0.707=-10lg2(dB)=-3dB,即增益降低到0.707倍(即-3dB),Θ=-arctan1=-45°
w=+∞时,|C|=0=-∞dB。Θ=-arctan(+∞)=-90°
以w的10倍分析:
w=1/10RC,1+(wRC)^2=1.01,则|C|=0.995=-0.043dB,Θ=-arctang(0.1)=-5.7°
w=1/RC,1+(wRC)^2=2,则|C|=0.707=-3dB,Θ=-arctang(1)=-45°
w=10/RC,1+(wRC)^2=101,则|C|=0.0995=-20dB,Θ=-arctang(10)=84.3°
w=100/RC,1+(wRC)^2=10001,则|C|=0.00995=-40dB,Θ=-arctang(100)=89.4°
w=1000/RC,1+(wRC)^2=1000001,则|C|=0.000995=-60dB,Θ=-arctang(1000)=89.9°
由上可知,在极点处前后10倍频,幅度降低3dB,相位变化为前后约45°。从相位上看,由于相位纵坐标为度数,所以前10倍频(0.1)平台开始降低45°,到达极点,继续往45°的趋势下降,直到下降了45°后不再下降,变为平台。在进入平台前,遇到零极点,则交点处开始下降45°,直到零极点,然后往45°趋势走,重复上步骤。
对于简单的RC低通电路,来说初始情况下,输出与输入相位相同,起始相位为0°;对于RC高通电路,由于电容作用,起始相位反相为180°。
对于正向放大电路,输出与输入同相,起始相位为0°;对于反向放大电路,输出与输入反相,起始相位为180°。
由于H(jw)=H(s),计算出的极点刚好与截止频率处一样(截止频率为1/2piRC)。
高通RC电路,则是极点为1/RC,截止频率也是,但是相位变化相反。
故可以通过BODE图(幅频特性),结合幅度变化、相位变化得到极点和零点。
根据控制系统原理,反馈回路可以等效为以下模型。
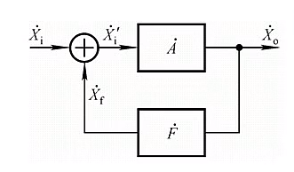
A为开环增益,F为反馈增益。求得闭环增益为(假定为负反馈):
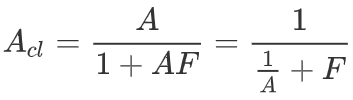
当AF=-1时,闭环增益无穷大,系统振荡。
可知,闭环增益≤开环增益。
对于运放来说,运放增益为Aol,反馈增益为β,则公式(已考虑β是负反馈,使用了-β)变为:
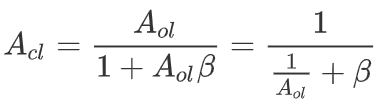
环路增益(开环增益)为Aolβ。当Aolβ=1,相位反相时,系统振荡。此时20lg(Aolβ)=0dB,相位变化180°。
当Aol极大(>10,即20dB)时,Acl≈1/β。
运放的增益与频率成反比关系,频率越高增益越低^1,它们之间的关系是运放的增益带宽积GBP^3。
运放的增益在低频时几乎为常数,穿越-3dB后为增益带宽积。
根据Nyquist判据,闭环传递函数、开环传递函数为:

对于运放来说:G(s)=Aol,H(s)=β,则F(s)=1+Aolβ。其中H(s)为反馈环增益。
Aol为运放本身的增益,可以通过芯片手册上的开环增益曲线估算其Aol(s),β为反馈增益即输出反馈给输入的信号增益。
以简单的反相放大电路为例,如下图所示。
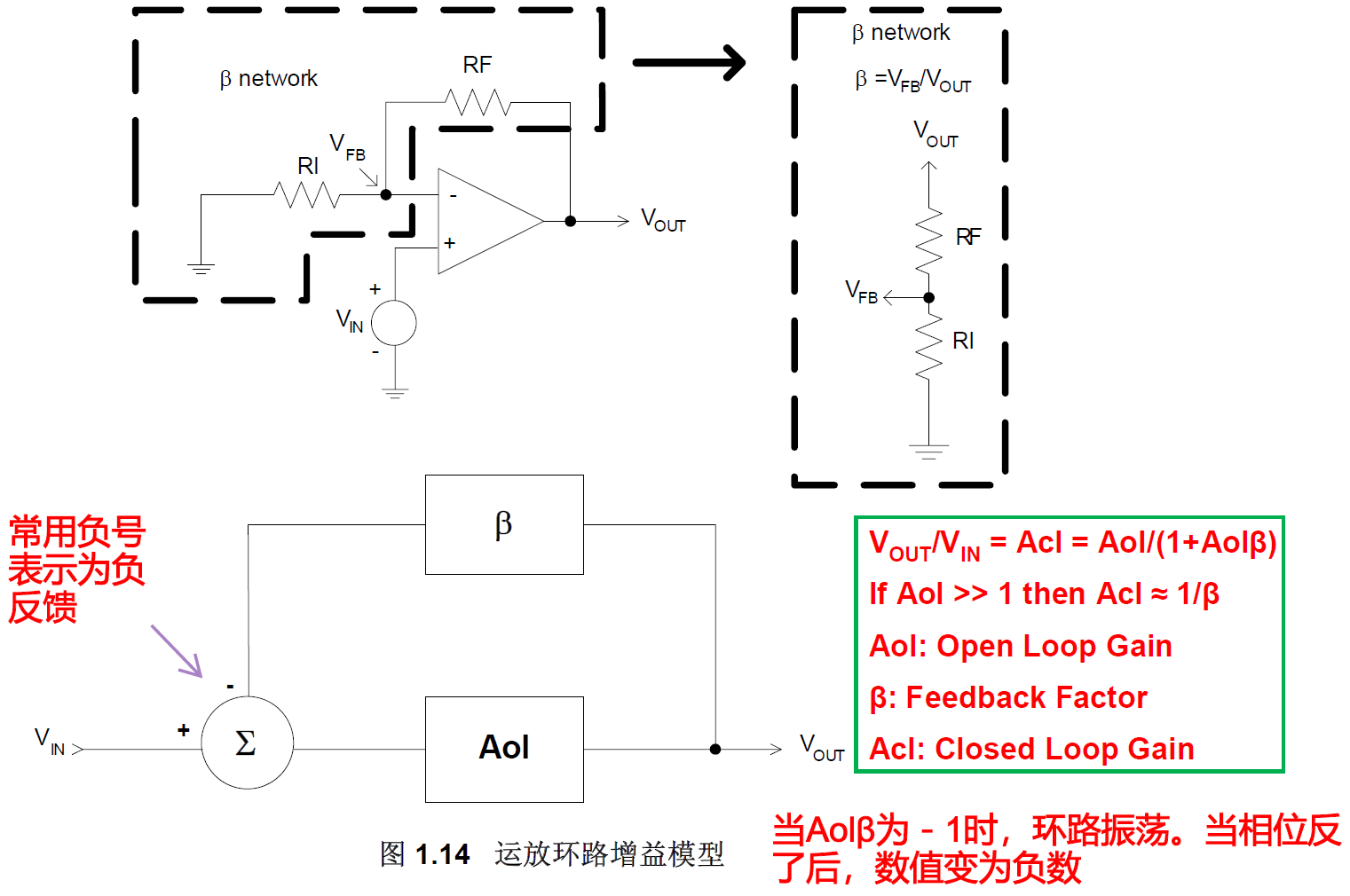
上图中,1/β做了近似,实际1/β应该为:
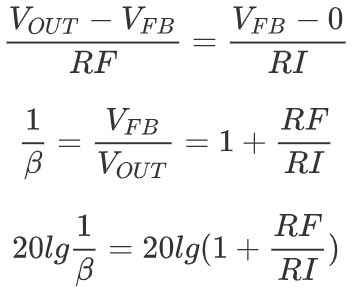
由于RF、RI均为正数,故1/β最小为1。假如RF和RI中存在电容,则在BODE图中表现为1/β曲线最小接近0dB,且为正数。
举例,某运放的Aol截止频率为1.59Hz,低频增益为59.03dB=900534倍,1/β=(1+RF/RI)=1001。则开环传递函数(运放的开环增益)的极点为w=2x3.14x1.59=10(1+Ts=sT+1,当s=jw=1/T时无穷大,截止频率为1/T,故T=1/w=0.1),增益k=900534。则运放的开环传递函数为:
$A_{ol}(s)=\frac{900534}{1+0.1s}$
$F(s)=1+A_{ol}(s)\beta=1+\frac{900534}{1+0.1s}$
使用TI-TINA仿真,结果如下图所示,将其与Matlab仿真结果(程序文件见^4)放一起对比。

在10k电阻上并联1uF电容,再次仿真,如下图所示。
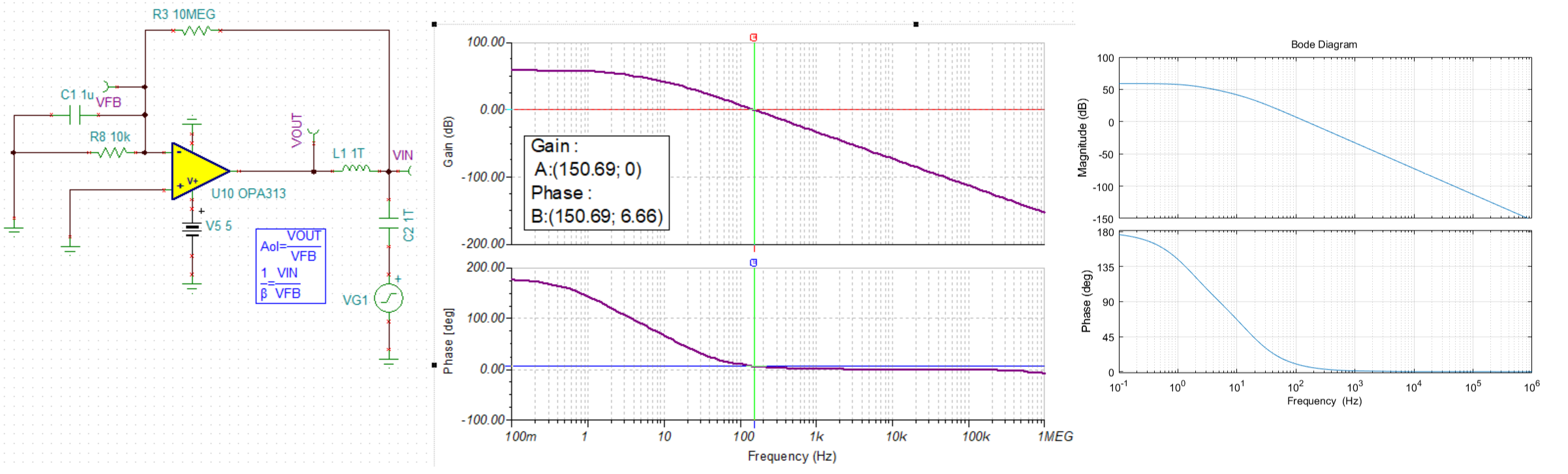
并联1uF后,运放的Aol不变,1/β=(1+RF/RI)的RI为C1和R8的并联,β为:
$\beta=\frac{RI}{RF+RI}=\frac{1}{\frac{RF}{RI}+1}=\frac{1}{\frac{R3}{\frac{1}{sC1}||R8}+1}=\frac{1}{10s+1001}$
开环传递函数为Aolβ:
sys =
900
----------------------
0.001 s^2 + 0.11 s + 1
Continuous-time transfer function.
有2个极点(-10和-100),为负数都在左半平面。观察Nyquist[^5]曲线,如下图所示。
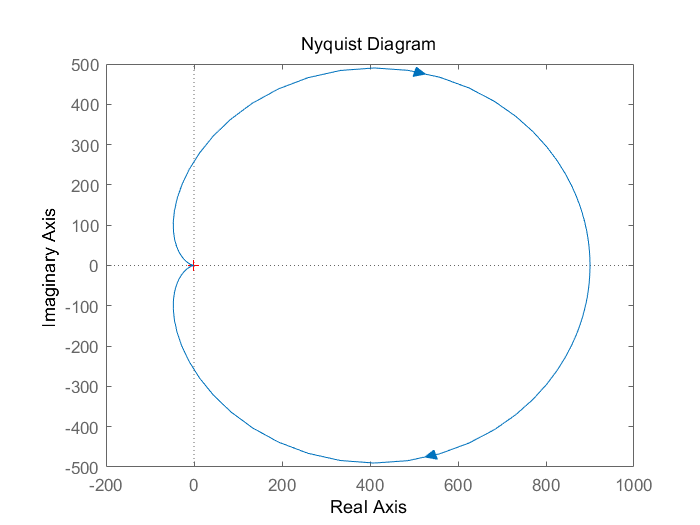
曲线不包含(-1,j0),故N=N+-N-=0-0=0。由于右半平面极点P为0(都在左半平面),故Z=P-2N=0-2*0=0可见闭环系统稳定(上图中有镜像)。
这里简要说下Nyquist稳定性判据:
Nyquist曲线为G(s)H(s)开环传递函数
F(s)=1+G(s)H(s)是G(s)H(s)往左边移动1个单位,故其穿越(0,j0)与G(s)H(s)穿越(-1,j0)等效
右半平面是不能有闭环极点的,也就是Z=0,这个闭环极点就是F(s)零点,或者说闭合曲线包围函数F(S)= 1+ G(s)*H(s)的零点数即反馈控制系统正实部极点数为Z=P-R=P-2N
P为开环传递函数右半平面极点数,N为绕(-1,j0)穿越圈数,(-1,j0)左边自上而下为正N+,右边则为负N-
判定的稳定性为闭环传递函数,不是开环传递函数
以上闭环传递函数Acl为:
sys3 =
9005 s + 900534
------------------------
0.001 s^2 + 0.11 s + 901
Continuous-time transfer function.
脉冲响应曲线为:
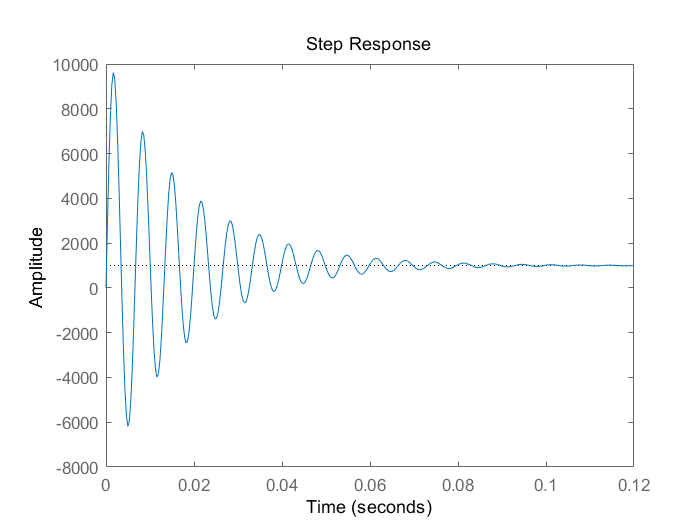
可见闭环传递函数脉冲响应阻尼振荡稳定。
根据TI资料,观察Aol与1/β的ROC(闭合速率),闭环系统也是不稳定,如下图所示。
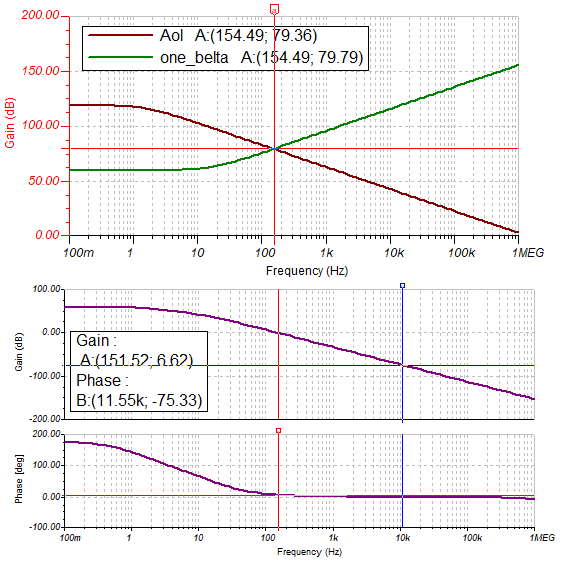
ROC(Aol-1/β)=40dB/Decade,为不稳定。
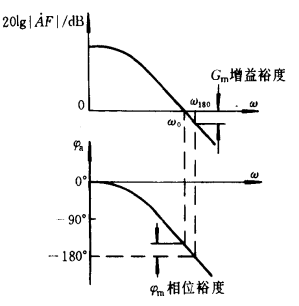
观察Aolβ的相位,可见在增益为0dB时,相位裕度只有6.6°,增益裕度为74dB,两者定义见下图。可见相位裕度很低(<45°),容易导致系统进入不稳定状态。
对于小信号的放大,一般认为在引入深度负反馈的情况下,在整个信号带宽内运放环路稳定,则电路设计没有问题。
对于Aolβ要求在相位为-180时,对应的|Aolβ|<1,其伯德图需要满足一定的增益和相位余量(>45度),见上图。
实际一般需要根据开环增益曲线Aol(由供应商的数据手册提供)和1/β增益曲线
(即噪声增益曲线,取决于反馈环路的设计)的交点判断,该交点决定了所能放大信号带宽,即闭环带宽fcl。
相位裕度和增益裕度都是穿越频率距离-180°(即不稳定处)的余量。
上例中闭环带宽为154.49Hz。
使用脉冲信号进行仿真脉冲响应,结果如下图所示。
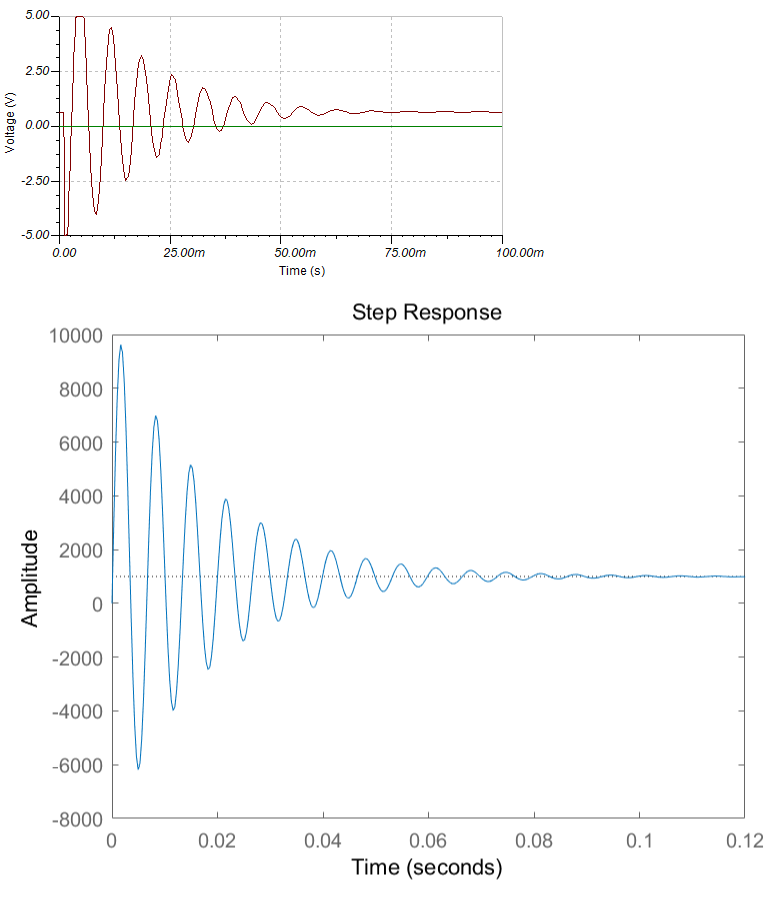
可见,系统在启动时会出现阻尼振荡。
因为BODE图(幅频、相位曲线)获取的关于稳定性的判断是相对稳定性,而不是绝对稳定性,Nyquist判据得出的为绝对稳定性。也可以说BODE的不稳定Nyquist可能为稳定,BODE的稳定Nyquist一定是稳定,即BODE图的判断条件范围小于Nyquist。换句话说就是,将BODE图判断不稳定的系统更改为稳定系统,则更改后系统一定稳定。
至此,可以使用BODE图来修正不稳定系统。
环路增益测试¶
常用的放大电路即为单端输入,上例即使如此。
测试系统稳定性时,只需将环路断开(断开反馈环路即可),变为开环系统,然后输入激励,获取Aol和1/β曲线。如下图所示。
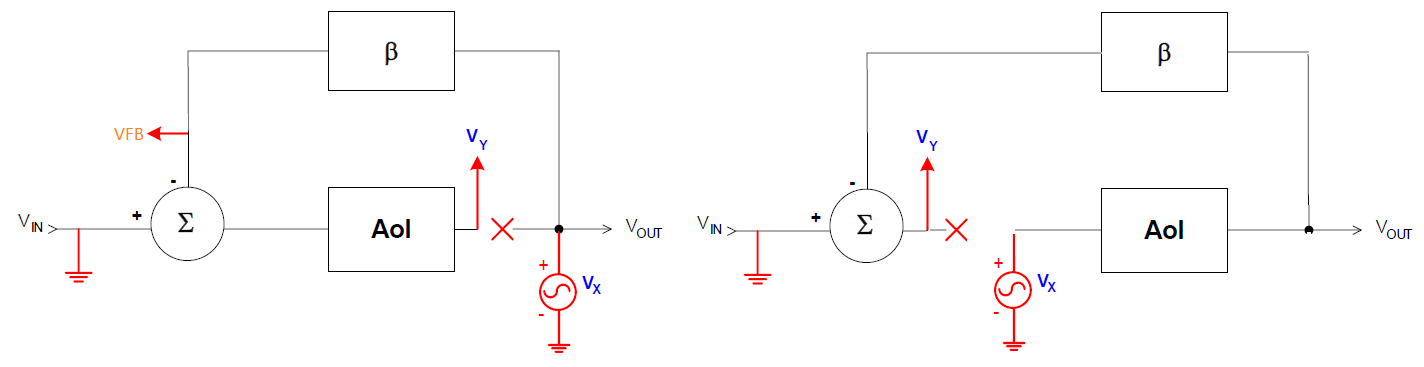
左边,断开输出到反馈的节点;右边断开反馈到输入的节点。环路增益均为:Aolβ=Vy/Vx。
左边:Aol=Vy/VFB,1/β=Vx/VFB
右边:Aol=Vout/Vx,1/β=Vout/Vy
用上例的电路^6分别做两种环路增益仿真,如下图所示。
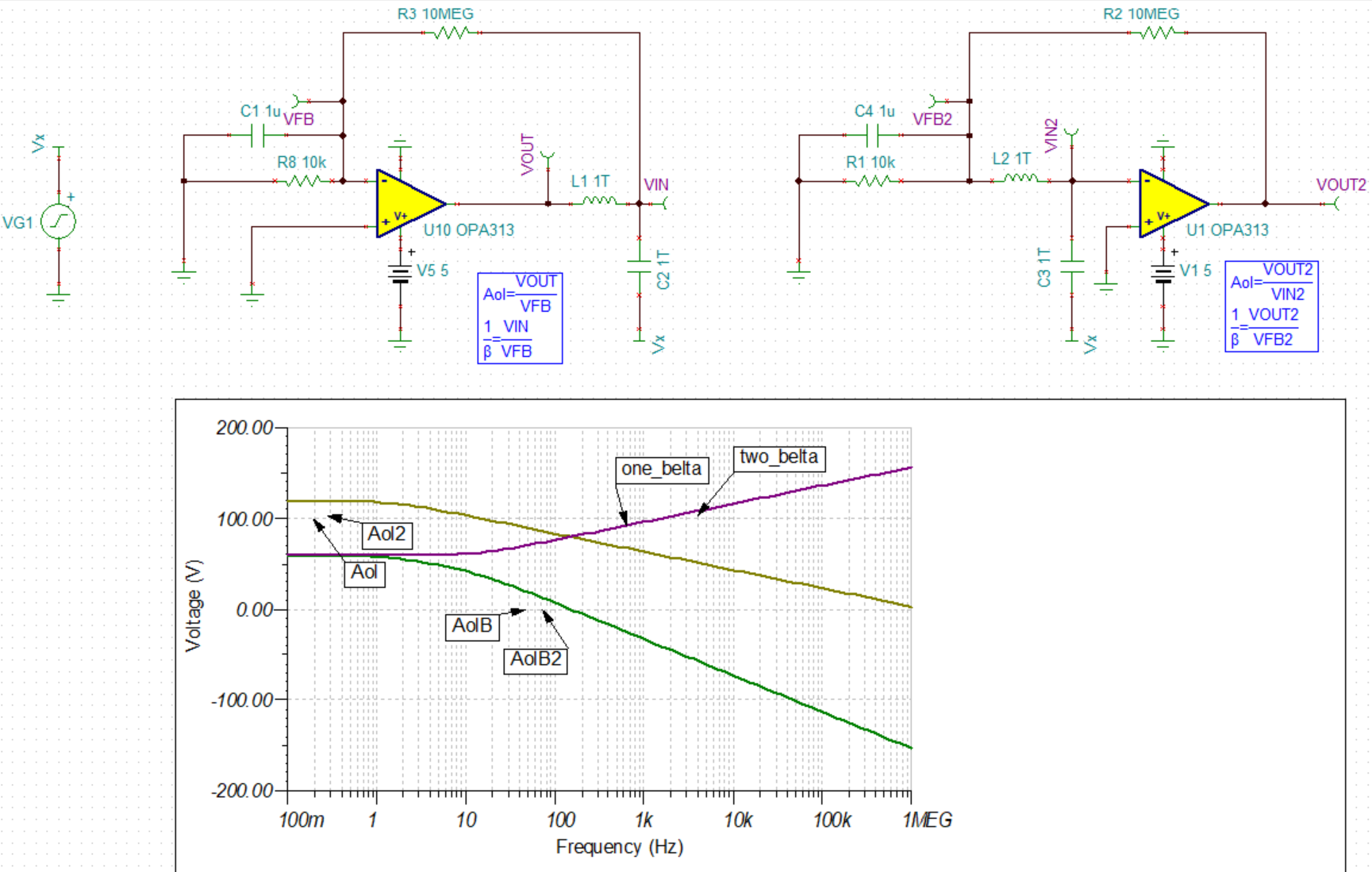
可见,仿真结果一样。
不加电容补偿时,1/β为直线,电容增加了β极点(1/β零点),BODE图上表现为1/β上翘。
由于Aol为运放固有特性,所以其一直不变,只需要观察1/β曲线即可。对于复杂的电路来说,反馈环路复杂,零极点很多。需要在Aol与1/β交点(Aolβ=0dB,fcl处,闭环穿越频率点)前将1/β拉直。