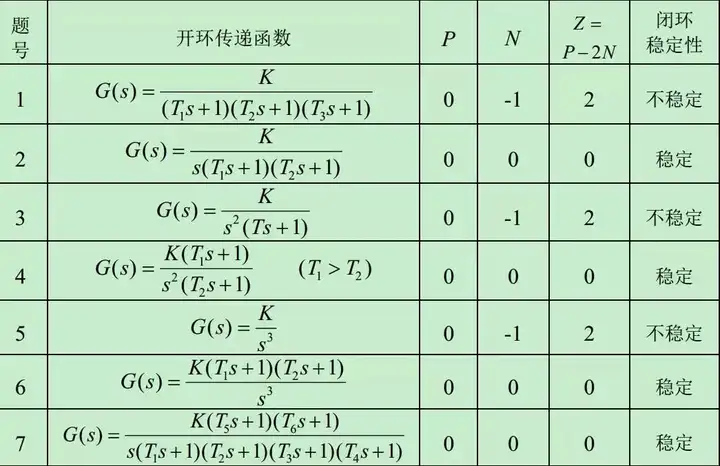
奈奎斯特稳定性判据

Nyquist稳定性判据：

  • Nyquist曲线为G(s)H(s)开环传递函数

  • F(s)=1+G(s)H(s)是G(s)H(s)往左边移动1个单位，故其穿越（0，j0）与G(s)H(s)穿越（-1，j0）等效

  • 右半平面是不能有闭环极点的，也就是Z=0，这个闭环极点就是F(s)零点，或者说闭合曲线包围函数F(S)= 1+ G(s)*H(s)的零点数即反馈控制系统正实部极点数为Z=P-R=P-2N

  • P为开环传递函数右半平面极点数，N为绕（-1，j0）穿越圈数，（-1，j0）左边自上而下为正N+，右边则为负N-

  • 判定的稳定性为闭环传递函数，不是开环传递函数

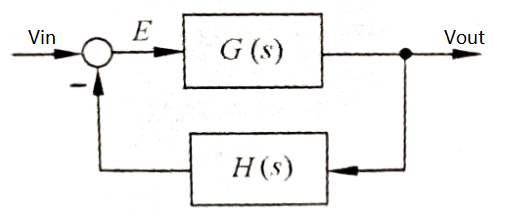
image-20230612223901301

以上是一个反馈系统，推算过程如下：

$(Vin-H(s)Vout)G(s)=Vout$

$\phi(s)=\frac{Vout}{Vin}=\frac{G(s)}{1+G(s)H(s)}$

其中开环传递函数为G(s)H(s)。定义的F(s)=1+G(s)H(s)。

闭合曲线包围F(s)平面原点的圈数等价于闭合曲线GH包围F(s)平面点(-1 , j0) 的圈数。

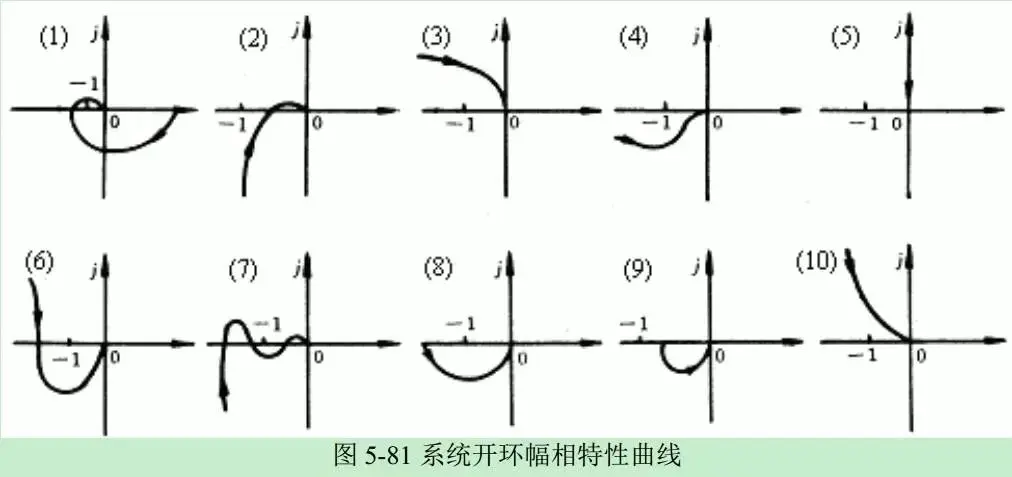
通过10个示例^1说明，以下是各图判断结果。

其中K，T都是正数。另外G(s)必须有分母。

下图中的G(s)就是G(s)H(s)。

https://pic2.zhimg.com/80/v2-f5f8faf9d4a61967b716e0c78d7a6ec9_720w.webp

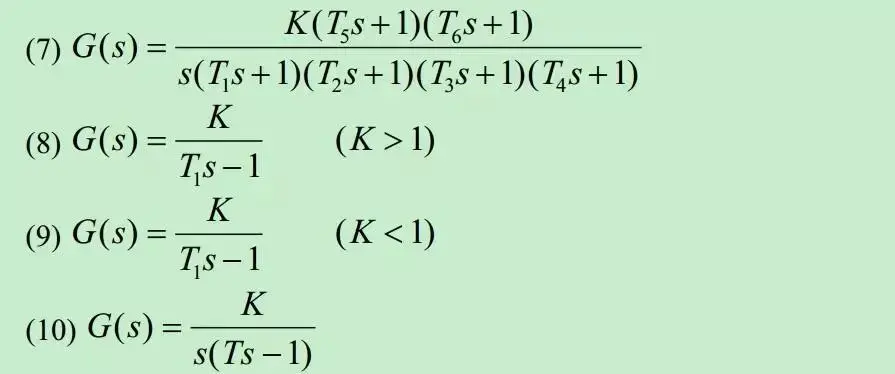
https://pic4.zhimg.com/80/v2-7ce78bf4b8c9a76f52229bae4ccc10df_720w.webp

https://pic4.zhimg.com/80/v2-c9cbada3990608f889df937a2eba47ef_720w.webp

https://pic2.zhimg.com/80/v2-ad22965edb5aaefa059284b269042181_720w.webp

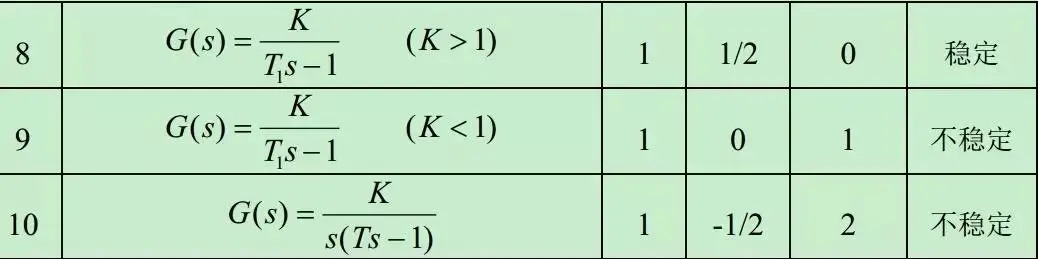
https://pic4.zhimg.com/80/v2-8566498385b3a29db4946f299ec3160f_720w.webp

（1）例

$G(s)=\frac{K}{(T_1s+1)(T_2s+1)(T_3s+1)} $

K=100;
T1=10;
T2=1.3;
T3=0.4;
num = [K]
Gs = tf(K,conv([T1,1],[T2,1]));
%open trasnfer function
Gopen = Gs*Hs;
%close transfer function
Gclose = Gs/(1+Gopen);

nyquist(Gopen)
%rlocus(Gopen)
%pzmap(Gopen)
step(Gclose)

img

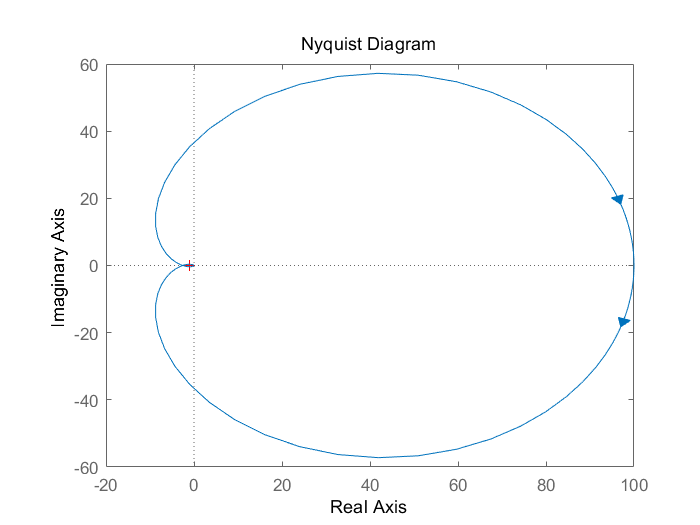
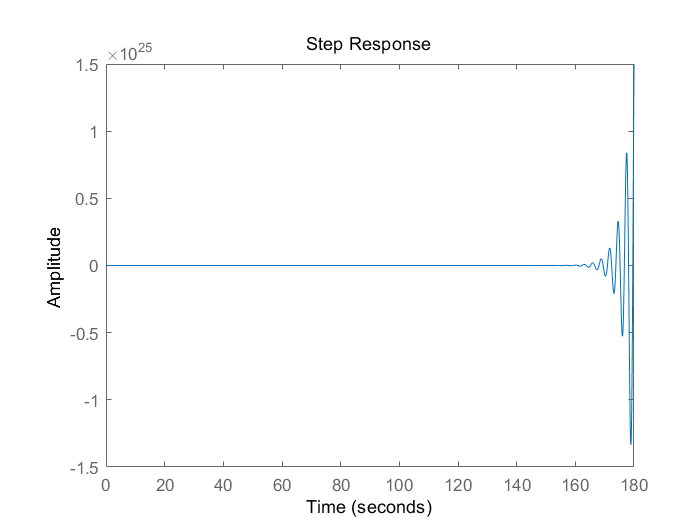
右半极点数P=0 Nyquist曲线上，从下向上在(-1,j0)左边穿越1圈，则N-=1，则Z=P-2(N+-N-)=0-2*(-1)=2。 故不稳定，脉冲响应如下。

img

（2）例

$G(s)=\frac{K}{s(T_1s+1)(T_2s+1)} $

K=2;
T1=1;
T2=0.3;
Gs = tf(K,conv([T1,1],[T2,1]))
Hs = tf([1],[1,0])
%open trasnfer function
Gopen = Gs*Hs
%close transfer function
Gclose = Gs/(1+Gopen)

nyquist(Gopen)
step(Gclose)

img

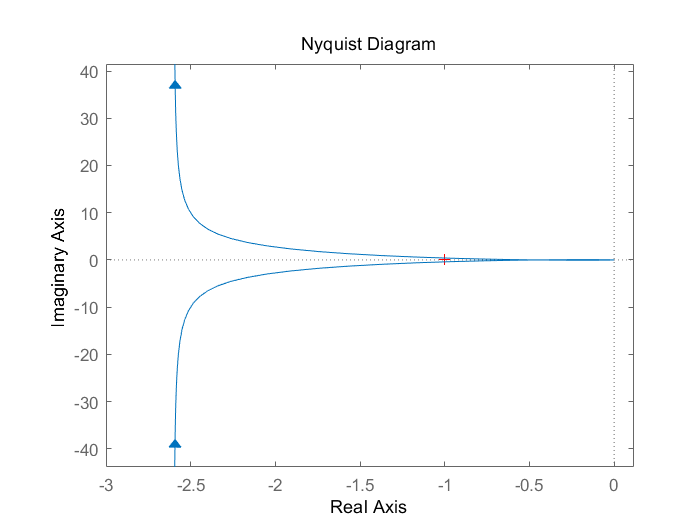
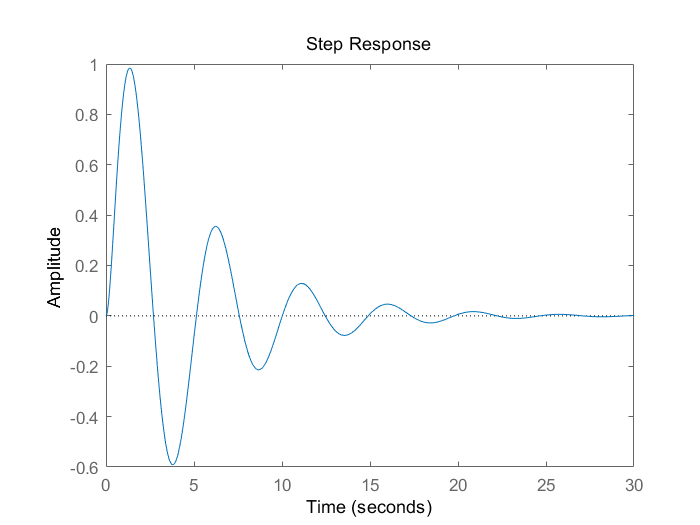
右半极点数P=0 半Nyquist曲线上，在(-1,j0)左边未穿越，则N=0 故Z=P-2(N+-N-)=0-2*(0)=0 故稳定，脉冲响应如下。

img

（3）例

$G(s)=\frac{K}{s^2(T_1s+1)} $

K=2;
T1=1;
Gs = tf(K,[T1,1])
Hs = tf([1],[1,0,0])
%open trasnfer function
Gopen = Gs*Hs
%close transfer function
Gclose = Gs/(1+Gopen)

nyquist(Gopen)
step(Gclose)

img

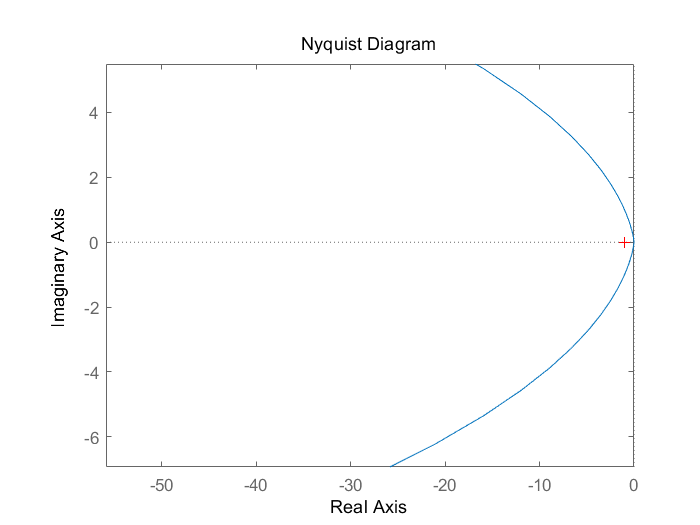
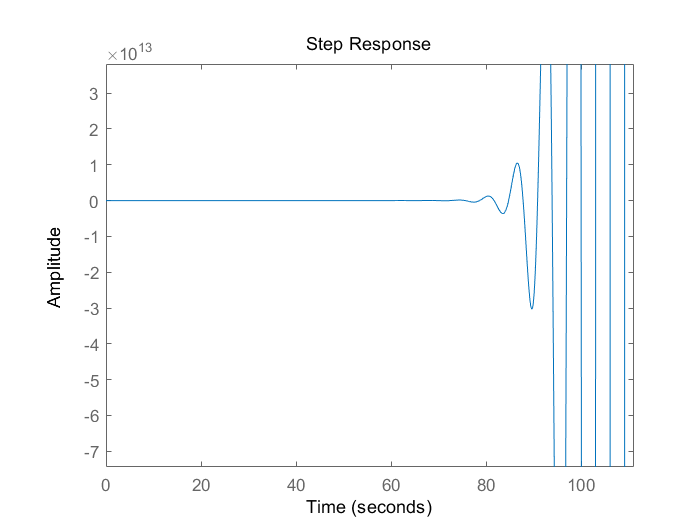
右半极点数P=0 半Nyquist曲线上，在(-1,j0)左边穿越1圈，则N-=1 故Z=P-2(N+-N-)=0-2*(-1)=2 故不稳定，脉冲响应如下。

img

（4）例

$G(s)=\frac{K(T_1s+1)}{s^2(T_2s+1)} (T1>T2)$

K=2;
T1=1;
T2=0.6;
Gs = tf(K,conv([1,0,0],[T2,1]))
Hs = tf([T1,1],[1])
%open trasnfer function
Gopen = Gs*Hs
%close transfer function
Gclose = Gs/(1+Gopen)

nyquist(Gopen)
step(Gclose)

img

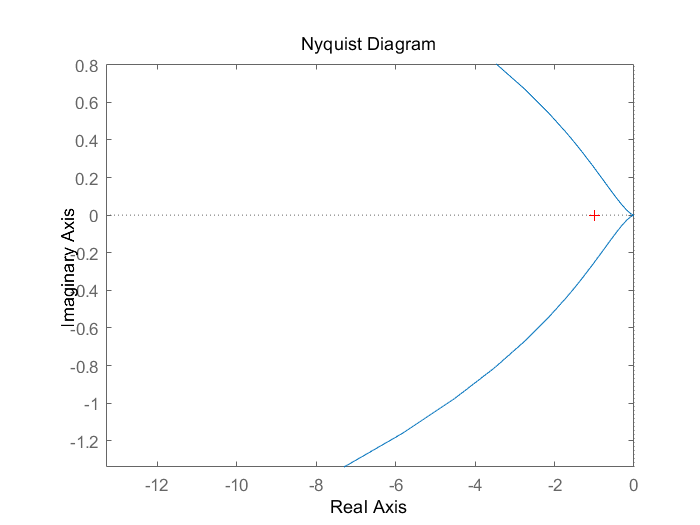
右半极点数P=0 在Nyquist曲线上，在(-1,j0)左边穿越0圈，则N-=0 故Z=P-2(N+-N-)=0-2*(0)=0 故稳定，脉冲响应如下。

img

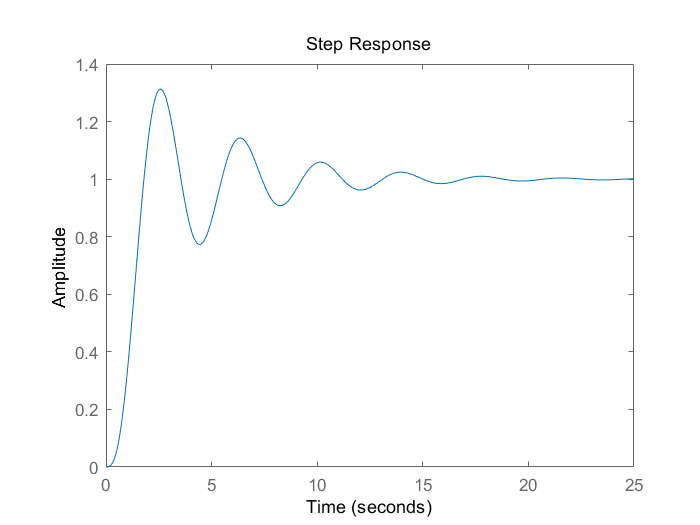
（5）例

$G(s)=\frac{K}{s^3} $

K=2;
Gs = tf([K],[1,0,0])
Hs = tf([1],[1,0])
%open trasnfer function
Gopen = Gs*Hs
%close transfer function
Gclose = Gs/(1+Gopen)

nyquist(Gopen)
step(Gclose)

img

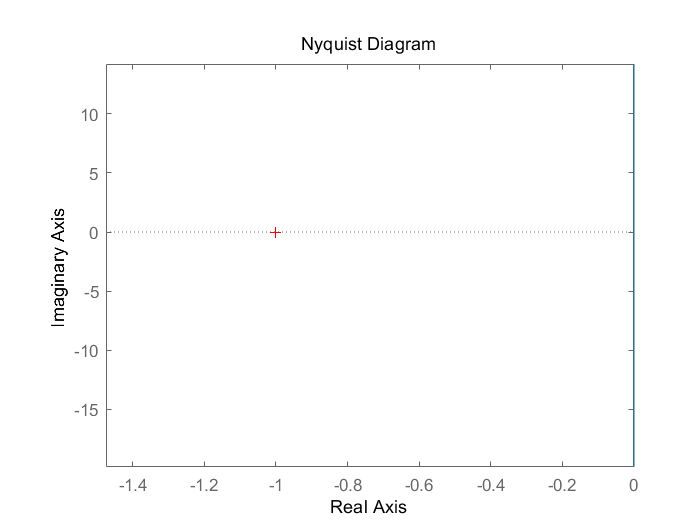
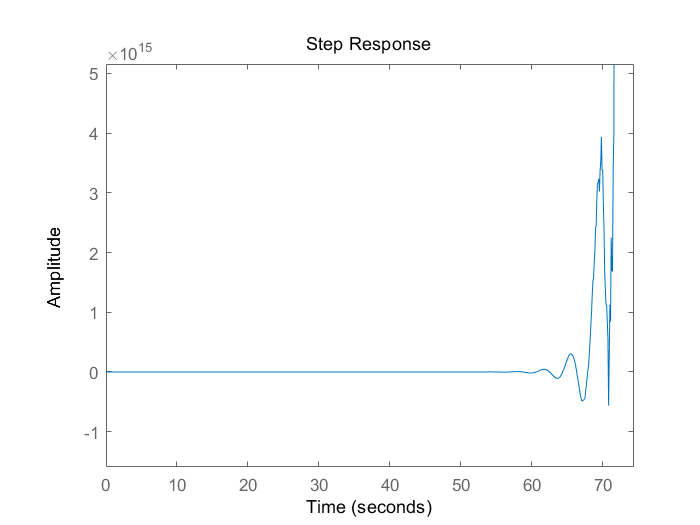
右半极点数P=0 在Nyquist曲线上，在(-1,j0)左边穿越1圈，则N-=1 故Z=P-2(N+-N-)=0-2*(-1)=2 故不稳定，脉冲响应如下。

img

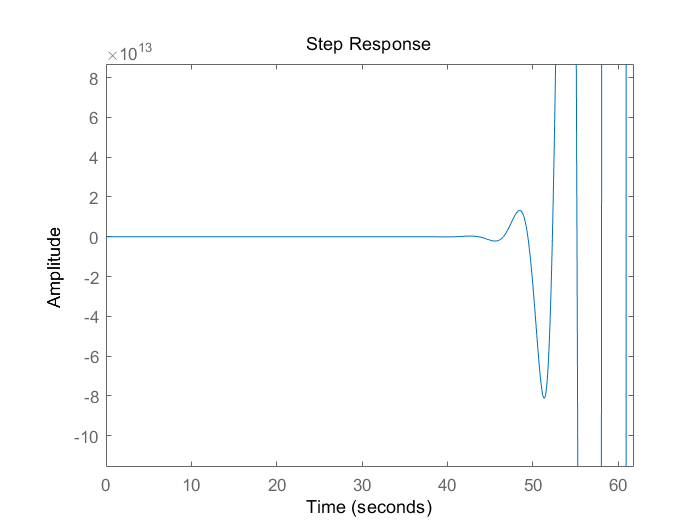
（6）例

$G(s)=\frac{K(T_1s+1)(T_2s+1)}{s^3} $

K=2;
T1=1;
T2=0.7;
Gs = tf(K*[T1,1],[1,0])
Hs = tf([T2,1],[1,0,0])
%open trasnfer function
Gopen = Gs*Hs
%close transfer function
Gclose = Gs/(1+Gopen)

nyquist(Gopen)
step(Gclose)

img

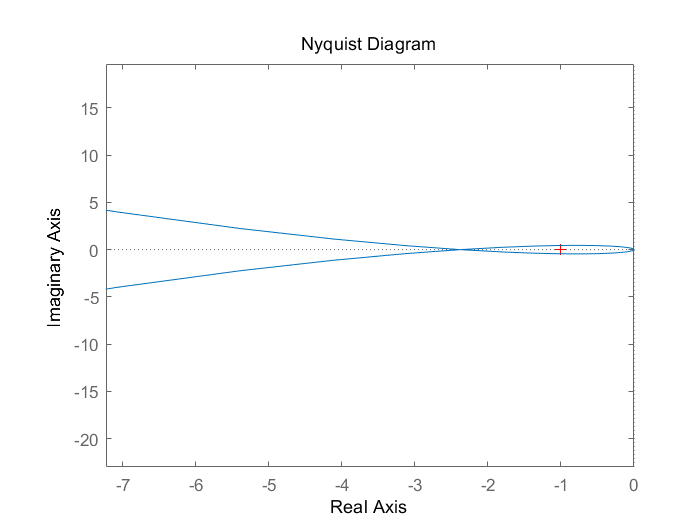
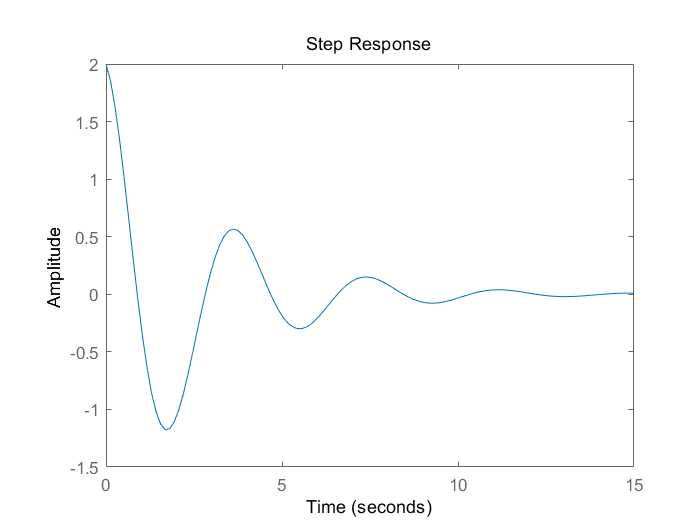
右半极点数P=0 在Nyquist曲线上，在(-1,j0)左边向上穿越1圈，向下穿越1圈，则N+=N-=1 故Z=P-2(N+-N-)=0-2*(1-1)=0 故稳定，脉冲响应如下。

img

（8）例

$G(s)=\frac{K}{T_1s-1} (K>1)$

K=3;
T1=2;

Gs = tf(K,[T1,-1])
Hs = 1
%open trasnfer function
Gopen = Gs*Hs
%close transfer function
Gclose = Gs/(1+Gopen)

nyquist(Gopen)
step(Gclose)

img

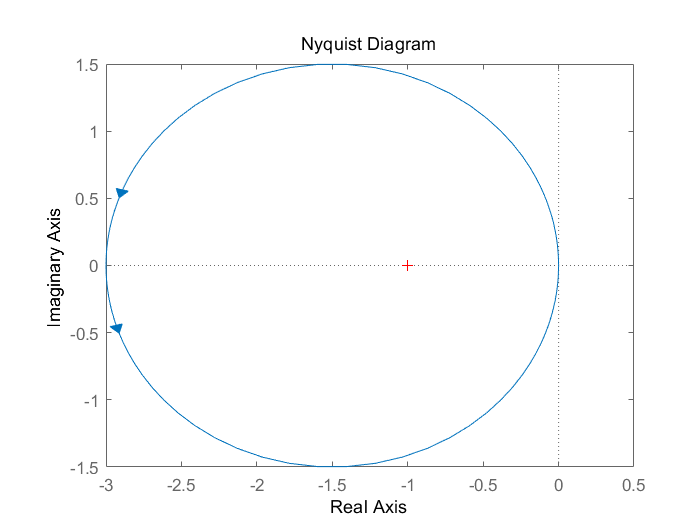
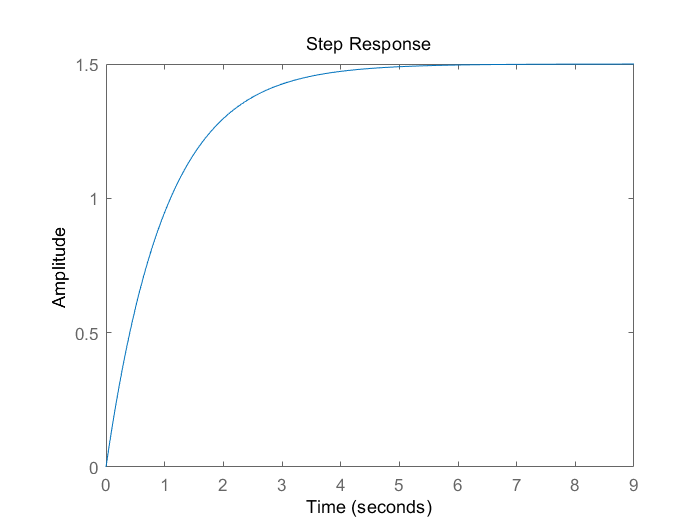
右半极点数P=1 在Nyquist曲线上，在(-1,j0)左边向下穿越1/2圈，则N+=1/2 故Z=P-2(N+-N-)=1-2*(1/2-0)=0 故稳定，脉冲响应如下。

img

（9）例

$G(s)=\frac{K}{T_1s-1} (K<1)$

K=0.3;
T1=2;

Gs = tf(K,[T1,-1])
Hs = 1
%open trasnfer function
Gopen = Gs*Hs
%close transfer function
Gclose = Gs/(1+Gopen)

nyquist(Gopen)
step(Gclose)

img

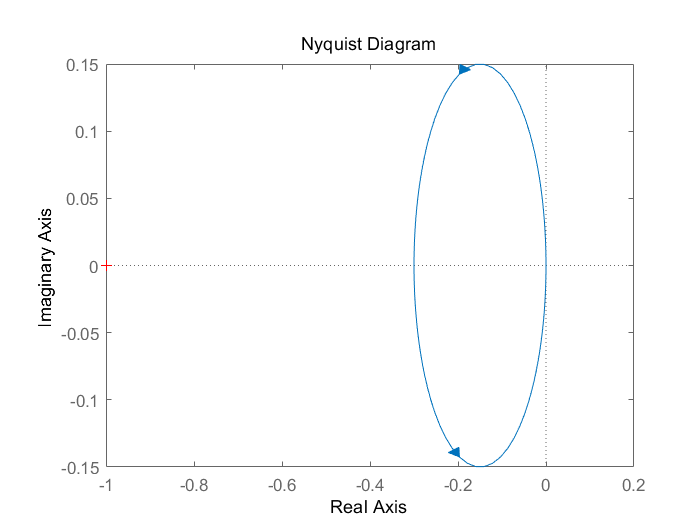
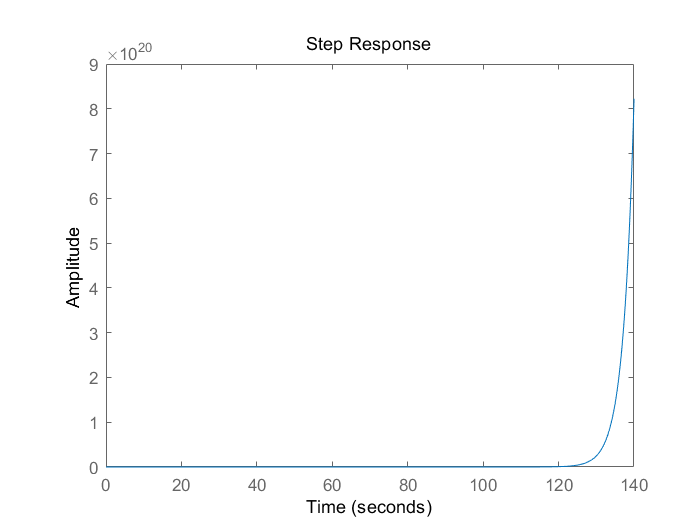
右半极点数P=1 在Nyquist曲线上，在(-1,j0)左边向下穿越0圈，则N+=0 故Z=P-2(N+-N-)=1-2*(0)=1 故不稳定，脉冲响应如下。

img

（10）例

$G(s)=\frac{K}{s(T_1s-1)}$

K=3;
T1=1;

Gs = tf(K,[T1,-1])
Hs = tf([1],[1,0])
%open trasnfer function
Gopen = Gs*Hs
%close transfer function
Gclose = Gs/(1+Gopen)

nyquist(Gopen)
step(Gclose)

img

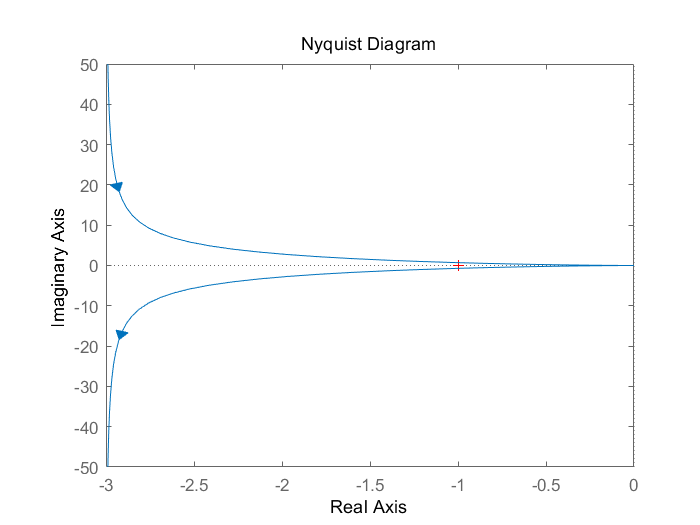
右半极点数P=1 在Nyquist曲线上，在(-1,j0)左边从下网上穿越1/2圈，则N-=1/2 故Z=P-2(N+-N-)=1-2*(0-1/2)=2 故不稳定，脉冲响应如下。

img

Reference